Prostor stanja problema kojeg rješavamo prikazuje se najčešće grafovima ili stablima.
Teorija grafova je oblast matematike, zastupljena u informatici i elektronici, čija je oblast istraživanje osobina grafova.
Proučavanje algoritama koji rješavaju probleme upotrebom grafova predstavlja značajan dio informatičke nauke.

Za prikaz prostora stanja problema koristit ćemo stablo pretraživanja:

• stanja – čvorovi -vrhovi stabla

• operatori grane (linije- lukovi) koji spajaju čvorove

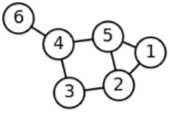Označeni graf sa 6 čvorova i 7 grana

Neformalno govoreći, grafovi su sastavljeni od tačaka, odnosno čvorova (vrhova), i linija među njima, odnosno grana. Grane (edge) predstavljaju vezu između čvorova grafa. Svaka grana spaja  dva čvora.

U računarstvu, graf je vrsta strukture podataka, tačnije apstraktan tip podataka, koji se sastoji od skupa čvorova i skupa grana, koje predstavljaju odnose (veze) između čvorova. Graf kao struktura podataka direktno potiče od matematičkog koncepta grafa.

Graf je uređena trojka G= (V;E;F) gdje je F funkcija koja svakoj grani E pridružuje 2-člani skup čvorova V.

Često (naročito kod neusmjerenih grafova) se isključuje funkcija koja definiše način pridruživanja čvorova pa se daje pojednostavljena definicija: Graf je uređen par G=(V,E), gdje je V(G) skup čvorova – vrhova (vertex), a E=E(G) skup grana-veza, bridova (edge).

U neusmjerenom grafu svaka grana predstavlja neuređeni par različitih čvorova: l_k=(n_i,n_j)

Neusmjereni graf (engl. undirected graph) predstavlja model mreže sa neusmjerenim vezama, odnosno, veza između entiteta postoji ili ne postoji. Neusmjerene veze se još nazivaju i simetrične veze, a takvi odnosi među entitetima najčešće opisuju srodstvo (npr. odnos „u vezi sa“, „u rodu sa“), interakcije (npr. „radi s“) ili neke zajedničke karakteristike (npr. „živi blizu“).

Neusmjereni graf G (N,L)   sastoji se od dva skupa informacija:

 - skupa čvorova: N={n₁,n₂,... n_k}; te

- skupa veza, odnosno grana,između parova čvorova: L={l₁,l₂,... l_n}

Grafovski algoritmi su od velikog značaja u računarstvu. Tipične operacije povezane sa grafovima su nalaženje puta između dva čvora, za šta se na primjer koriste pretraga grafa u dubinu i pretraga grafa u širinu, ili nalaženje najkraćeg puta od jednog do drugog čvora, za šta se može koristiti A star algoritam.

Praktična primjena

U praksi, za svaki čvor i granu vezujemo neke podatke sa kojima želimo da manipulišemo.

Mnoge se pojave modeliraju grafovima koji se sastoje od čvorova i grana (veza među čvorovima).

Na primjer, čvorovi mogu predstavljati ljude iz neke skupine, a grane (edge) parove prijatelja.

Graf može predstavljati električnu mrežu čiji su vrhovi električke komponente, a grane električne veze. Putne- cestovne, željezničke, avio veze itd. daljnji su primjeri modela s grafovima.

U računarstvu se često dijagram toka nekog algoritma prikazuje grafom kojem su čvorovi naredbe (instrukcije), a lukovi iz jedne u drugu naredbu su grane.

Jednako tako grafovima se prezentuju i razne računarske strukture podataka, umrežavanje i paralelizam računara i njihov sekvencijalni rad, evolucijska ili porodična stabla u biologiji itd.

Proučavanje algoritama koji rješavaju probleme upotrebom grafova predstavlja značajan dio informacionih nauka.