U slučaju logičke funkcije sa tri promjenljive postoji osam mintermova - osam polja

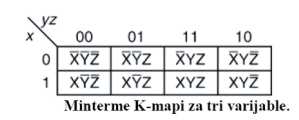
Primjenićemo istu ideju kao kod dvije varijable
Uočimo razlike: Prva razlika je da su dvije varijable grupisane zajedno u tablici. Druga je razlika u nizu brojeva dodijeljenih kolonama.
Prebrojavanje kolona nije sekvencijalno, prema prirodnoj binarnoj progresiji. (Ovo je posljedica demonstrirana razvojem u torus) Ulazne vrijednosti za K-mape moraju biti poredane tako da se svaka minterma razlikuje samo u jednoj varijabli u odnosu na susjedne minterme.
Zapamtite, da biste reducirali, potrebno je odbaciti varijablu koja se mijenja unutar grupe.
Moguće je imati grupe od četiri ili čak osam jedinica, zavisno od funkcije.

Primjer Pogledajte i analizirajte sliku koja ilustruje odnos tablice istinitosti i Karnove mape te način na koji se izvršila minimizacija Dvije jedinice u grupi omogućuju odbacivanje jedne varijable.

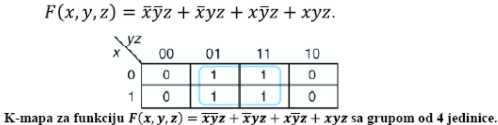
Kako pojednostaviti izraz kada imamo četiri jedinice u grupi? Četiri jedinice u grupi omogućuju nam odbacivanje dvije varijable: one dvije varijable kod kojih se sve četiri kombinacije razlikuju. Pogledajte i analizirajte primjer Sve imaju zajedničku varijablu z, a razlikuju se varijable x i y . Prema tome odbacujemo varijable x i y, pri čemu ostaje F(x,y,z) = z kao konačni rezultat minimizacije